

There you have it–the secant is the line from the center of the circle to the tangent line AC. The angle AOB appears in the triangle COA as angle AOC, so sec AOB = sec AOC = hyp/adj = OC/OA = OC. Next, to interpret secants geometrically. By symmetry the tangent of the angle FOB is the line FG, but FOB is the complementary angle of AOB, hence, the cotangent of AOB is FG. These other three functions can also be interpreted with the unit circle diagram. Note that cotangents are tangents of complementary angles, which means that cot A = tan B, and cosecants are secants of complementary angles, and that means that csc A = sec B. They’re pretty much redundant, but it’s worthwhile to know what they are in case you come across them. You can see by the listing that cotangent (abbreviated cot, or sometimes ctn) is the reciprocal of tangent, secant (abbreviated sec) is the reciprocal of cosine, and cosecant (abbreviated csc, or sometimes cosec) is the reciprocal of sine. There are six ways of making ratios of two sides of a right triangle, and that gives the six functions: You might ask, “why six trig functions?” It’s a kind of symmetry. There are, however, cases when some others are needed. The other three trigonometric functions: cotangent, secant, and cosecantįor most purposes the three trig functions sine, cosine, and tangent are enough. (If you like, you can convert the 0.79 degrees to minutes and seconds.) The arctangent of 0.2455 is 13.79, so the angle A is 13.79°. Usually there’s a button on the calculator labelled “inv” or “arc” that you press before pressing the appropriate trig button. On a calculator, we use the inverse trig functions named arctangent, arcsine, and arccosine. Back when people used tables of trig functions, they would just look up in the tangent table to see what angle had a tangent of 0.2455. Again, you use the trig functions, but in reverse. Now let’s look at the problem of finding angles if you know the sides. Inverse trig functions: arcsine, arccosine, and arctangent Whether you use a sine, cosine, or tangent depends on which side and angle you know. For example, if the side a = 15 and the angle A = 41°, we can use a sine and a tangent to find the hypotenuse and the other side. We might only know one side but we also know an angle.

Now suppose we know the hypotenuse and one side, but have to find the other. (It’s nice to give examples where the square roots come out whole numbers in life they usually don’t.)

The Pythagorean theorem will give us the hypotenuse. Suppose we don’t know the hypotenuse but we do know the other two sides.
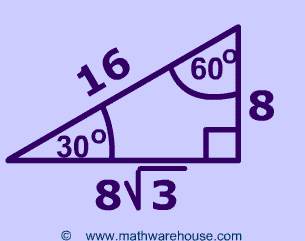
Let’s first look at some cases where we don’t know all the sides.
#Rules for special right triangles free#
If you want more than just these few free resources join the Geometry Teacher Community.We can use the Pythagorean theorem and properties of sines, cosines, and tangents to solve the triangle, that is, to find unknown parts in terms of known parts. They will learn the jingle whether they want to or not! Then watch their test scores and recall go up! Have them watch the video lesson on their own and then play the jingle throughout class over and over. They need to be able to create them but they are used so much that needing to memorize them is inevitable. Teaching the Unit Circle is hard enough if they haven't mastered the Special Right Triangles it becomes a nightmare! Special Right Triangles Worksheet and Guided Notesīelow are a Worksheet and Guided Notes to assist you in your lesson but one way I found very effective is to teach them a jingle to remember these few special triangles. Well, it's that time of the year! As you know your lesson on Special Right Triangles will not only be the foundation for everything trigonometry moving forward but it's also something that their Algebra 2, Pre-Calculus, and Calculus teachers are heavily relying on you to teach them.


 0 kommentar(er)
0 kommentar(er)
